Selection Sort

Selection sort is considered one of the fundamental sorting algorithms due to its simplicity and effectiveness. The way it operates is by iteratively identifying the smallest (or largest) element from the unsorted section of the list and relocating it to its correct position within the sorted portion of the list. This process continues until all elements are appropriately sorted, making it a reliable method for arranging data in ascending or descending order. The algorithm's straightforward nature and clear logic make it a popular choice for educational purposes and scenarios where simplicity and ease of implementation are prioritized.

The algorithm repeatedly selects the smallest (or largest) element from the unsorted portion of the list and swaps it with the first element of the unsorted part. This process is repeated for the remaining unsorted portion until the entire list is sorted.

Working of Selection Sort

1. Set the first element as minimum.

   

   Select first element as minimum

2. Compare minimum with the second element. If the second element is smaller than minimum, assign the second element as minimum.

   Compare minimum with the third element. Again, if the third element is smaller, then assign minimum to the third element otherwise do nothing. The process goes on until the last element.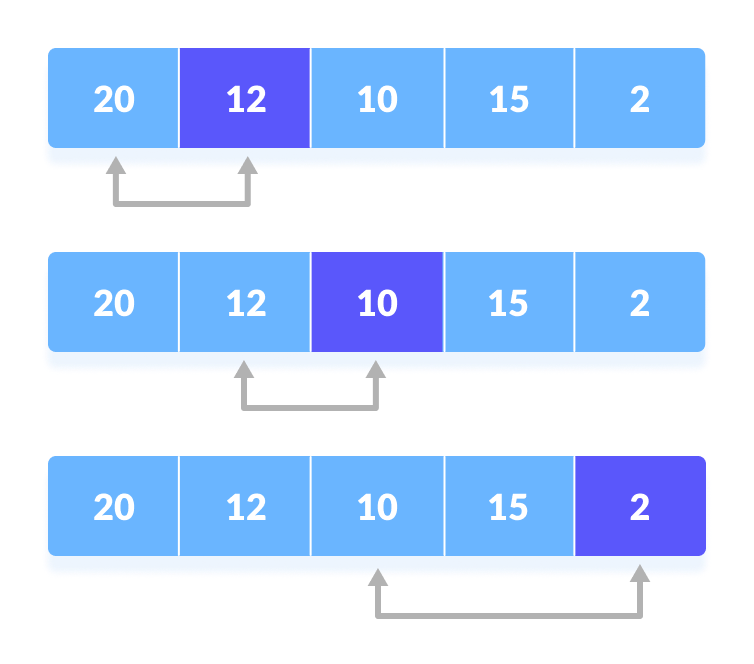

   

   Compare minimum with the remaining elements

3. After each iteration, minimum is placed in the front of the unsorted list.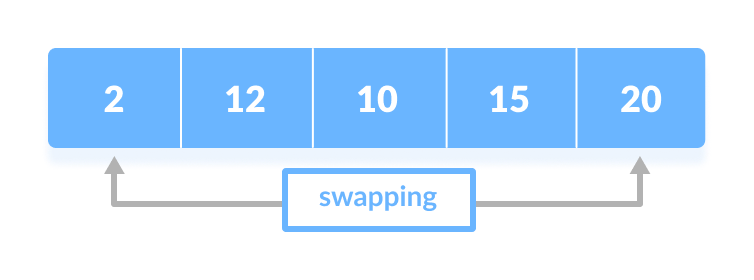

   

   Swap the first with minimum

4. For each iteration, indexing starts from the first unsorted element. Step 1 to 3 are repeated until all the elements are placed at their correct positions.

   

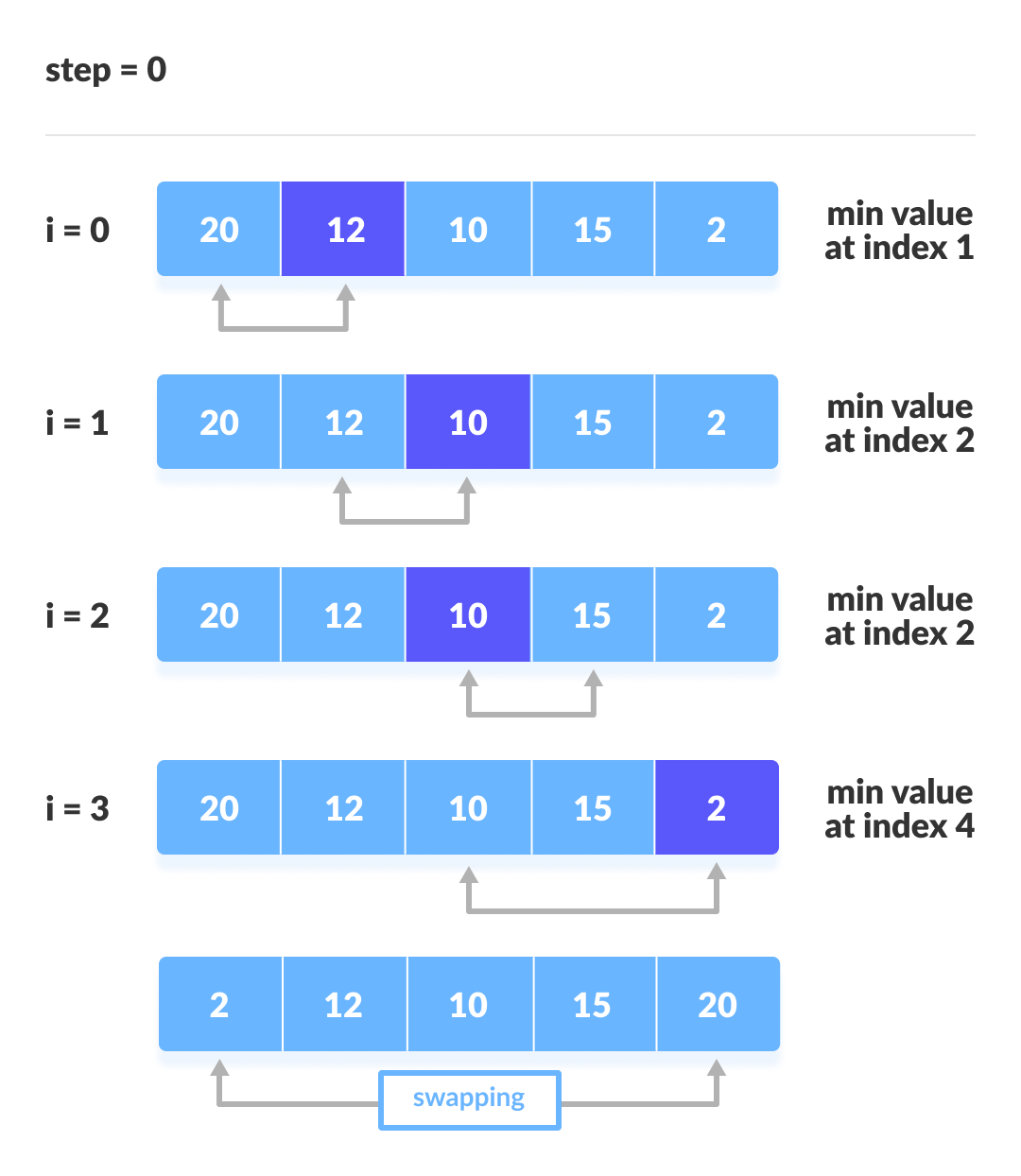
   The first iteration

   

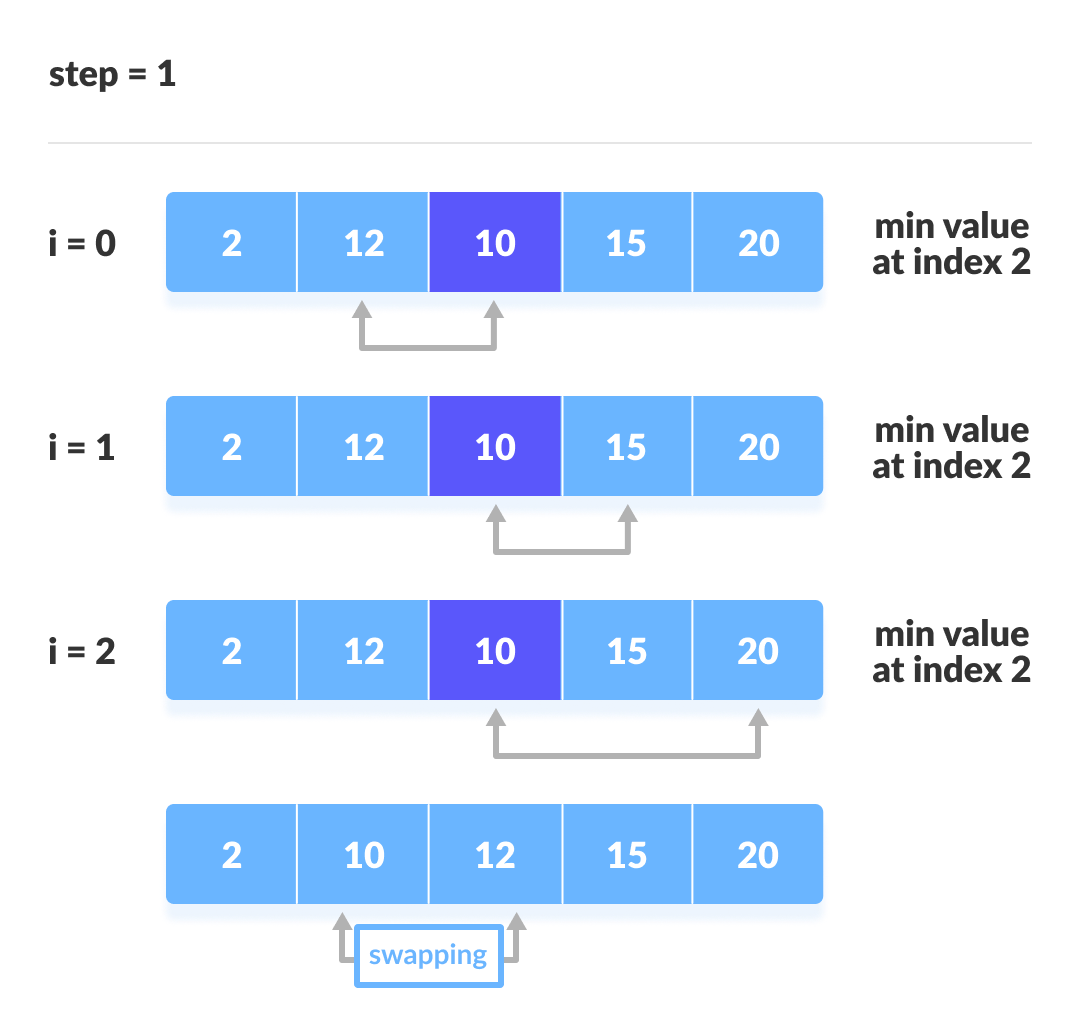
   The second iteration

   

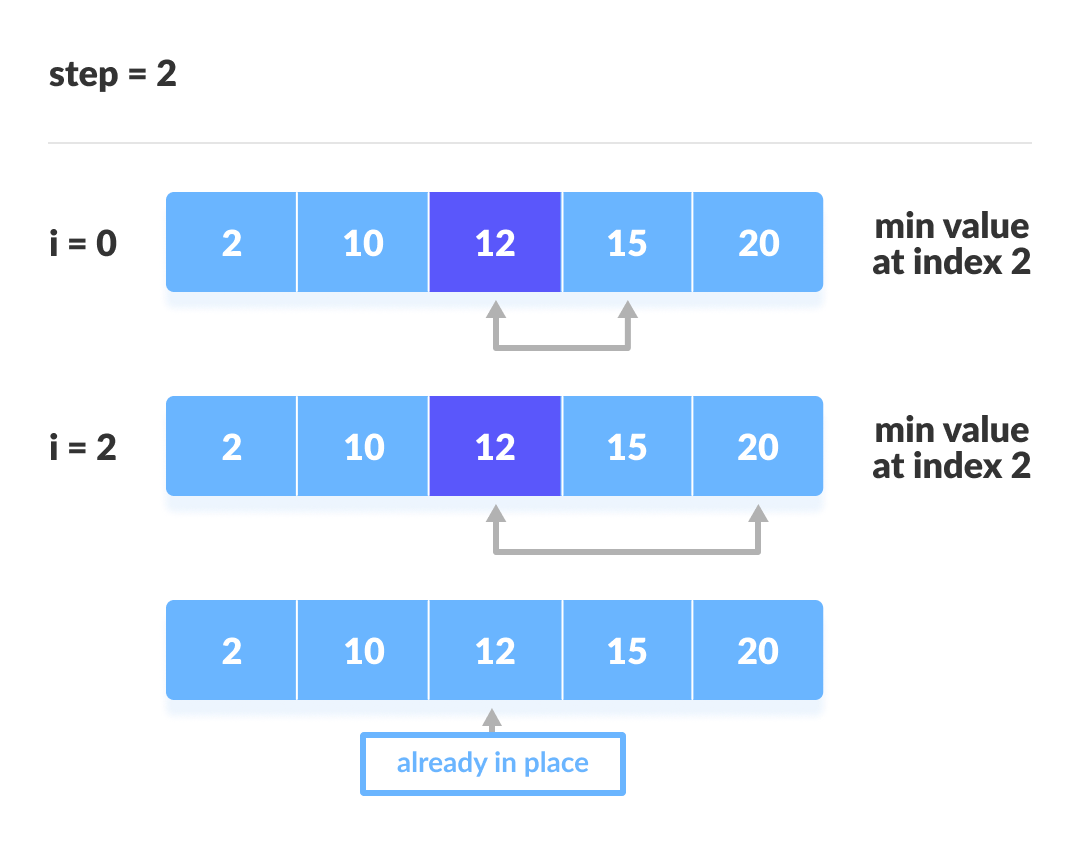
   The third iteration

   

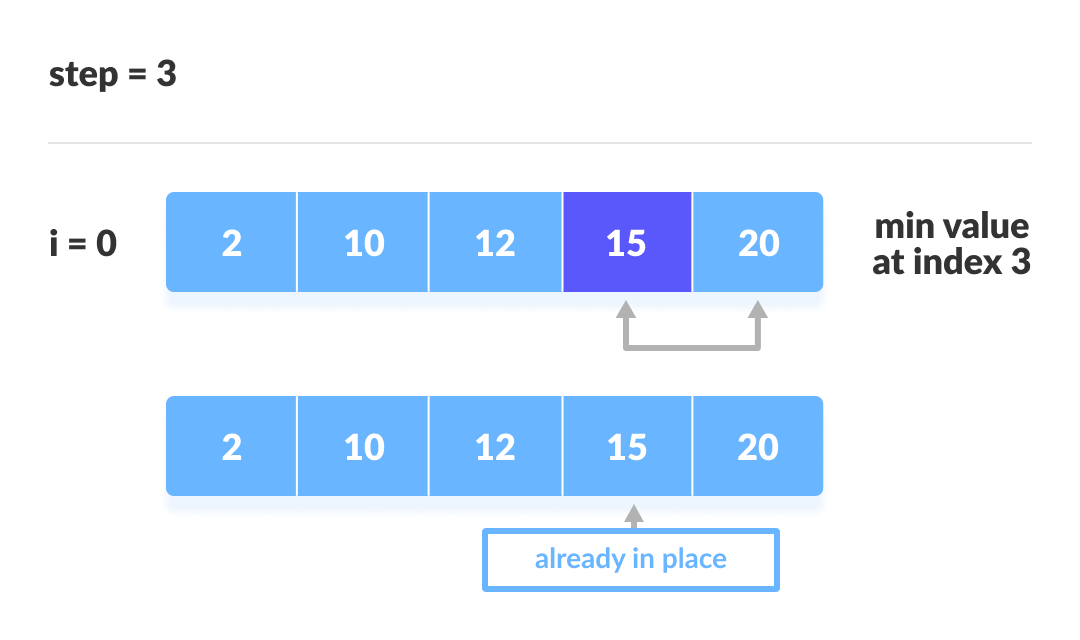
   Complexity Analysis of Selection Sort

   Time Complexity: The time complexity of Selection Sort is O(N2). This is because there are two nested loops involved:

   • One loop to select an element of the Array one by one, which takes O(N) time.

   • Another loop to compare that element with every other Array element, also taking O(N) time.

Therefore, the overall complexity is calculated as O(N) * O(N) = O(N^2) = O(N2).

Auxiliary Space: The auxiliary space complexity is O(1) since the only extra memory used is for temporary variables during the swapping of two values in the Array. Selection sort never performs more than O(N) swaps and can be beneficial when writing to memory is expensive.

Advantages of Selection Sort Algorithm

• Simple and easy to understand.

• Works well with small datasets.

Disadvantages of the Selection Sort Algorithm

• Selection sort has a time complexity of O(n^2) in the worst and average case.

• Does not work well on large datasets.

• Does not preserve the relative order of items with equal keys which means it is not stable.