Radix Sort

In Radix sort, we sort numbers digit by digit, starting from the least significant digit to the most significant digit.

Radix sort is like sorting students' names alphabetically. There are 26 groups for the 26 letters in the alphabet. In the first pass, names are grouped by the first letter. In the second pass, names are grouped by the second letter, and so on, until the list is sorted.

The steps for Radix sort are:

• First, find the largest element (let's call it max) in the array. Suppose 'x' is the number of digits in max. We need 'x' because we will sort by each digit.

• Then, sort the array by each digit, one by one. Use any stable sorting algorithm to sort the digits at each place.

Now let's see how Radix sort works with an example. To understand it better, let's take an unsorted array and sort it using Radix sort. This will make the explanation clearer and easier.

In the given array, the largest element is 736 that have 3 digits in it. So, the loop will run up to three times (i.e., to the hundreds place). That means three passes are required to sort the array.

Now, first sort the elements on the basis of unit place digits (i.e., x = 0). Here, we are using the counting sort algorithm to sort the elements.

Pass 1:

In the first pass, the list is sorted on the basis of the digits at 0's place.

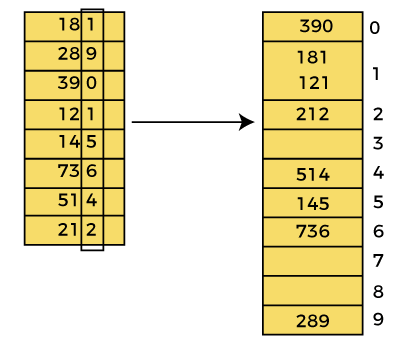
After the first pass, the array elements are -

Pass 2:

In this pass, the list is sorted on the basis of the next significant digits (i.e., digits at 10^th place).

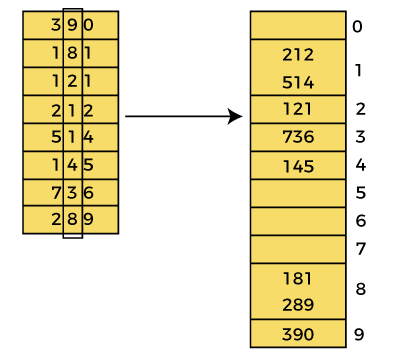
After the second pass, the array elements are -

Pass 3:

In this pass, the list is sorted on the basis of the next significant digits (i.e., digits at 100^th place).

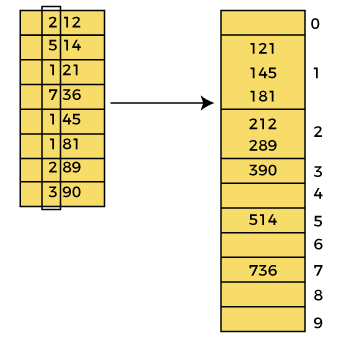
After the third pass, the array elements are -

Now, the array is sorted in ascending order.

Time Complexity:

• • Radix sort is a non-comparative integer sorting algorithm. It sorts data by grouping the keys based on their individual digits that share the same position and value. Its time complexity is O(d * (n + b)), where d is the number of digits, n is the number of elements, and b is the base of the number system used.

    • In practice, radix sort is often faster than other comparison-based sorting algorithms like quicksort or merge sort for large datasets, especially when the keys have many digits. However, its time complexity increases linearly with the number of digits, making it less efficient for small datasets.

Auxiliary Space:

• Radix sort also has a space complexity of O(n + b), where n is the number of elements and b is the base of the number system. This space complexity is due to the need to create buckets for each digit value and to copy the elements back to the original array after sorting each digit.