Quick Sort

The working procedure of Quicksort is also simple. This article will be very helpful and interesting to students as they might face quicksort as a question in their examinations. So, it is important to discuss the topic.

Sorting is a way of arranging items in a systematic manner. Quicksort is the widely used sorting algorithm that makes n log n comparisons in average case for sorting an array of n elements. It is a faster and highly efficient sorting algorithm. This algorithm follows the divide and conquer approach. Divide and conquer is a technique of breaking down the algorithms into subproblems, then solving the subproblems, and combining the results back together to solve the original problem.

Divide: In Divide, first pick a pivot element. After that, partition or rearrange the array into two sub-arrays such that each element in the left sub-array is less than or equal to the pivot element and each element in the right sub-array is larger than the pivot element.

Conquer: Recursively, sort two subarrays with Quicksort.

Combine: Combine the already sorted array.

Quicksort picks an element as pivot, and then it partitions the given array around the picked pivot element. In quick sort, a large array is divided into two arrays in which one holds values that are smaller than the specified value (Pivot), and another array holds the values that are greater than the pivot.

After that, left and right sub-arrays are also partitioned using the same approach. It will continue until the single element remains in the sub-array.

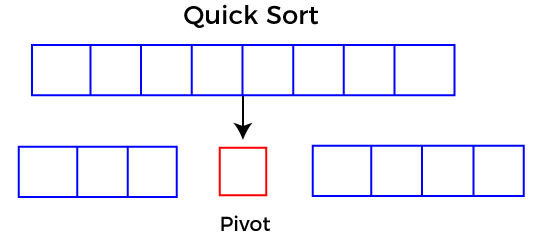
Choosing the pivot

Picking a good pivot is necessary for the fast implementation of quicksort. However, it is typical to determine a good pivot. Some of the ways of choosing a pivot are as follows -

• Pivot can be random, i.e. select the random pivot from the given array.

• Pivot can either be the rightmost element of the leftmost element of the given array.

• Select median as the pivot element.

• Working of Quick Sort Algorithm

  Now, let's see the working of the Quicksort Algorithm.

  To understand the working of quick sort, let's take an unsorted array. It will make the concept more clear and understandable.

  Let the elements of array are -

  

  In the given array, we consider the leftmost element as pivot. So, in this case, a[left] = 24, a[right] = 27 and a[pivot] = 24.

  Since, pivot is at left, so algorithm starts from right and move towards left.

  

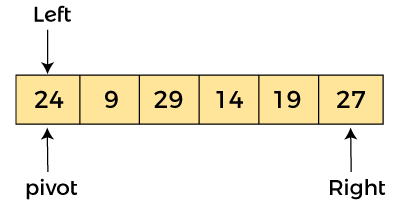
  Now, a[pivot] < a[right], so algorithm moves forward one position towards left, i.e. -

  ADVERTISEMENT

  

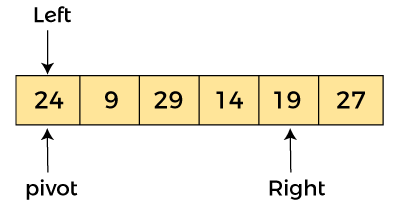
  Now, a[left] = 24, a[right] = 19, and a[pivot] = 24.

  Because, a[pivot] > a[right], so, algorithm will swap a[pivot] with a[right], and pivot moves to right, as -

  

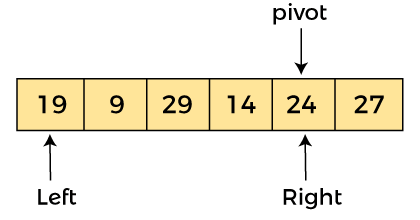
  ADVERTISEMENT

  Now, a[left] = 19, a[right] = 24, and a[pivot] = 24. Since, pivot is at right, so algorithm starts from left and moves to right.

  As a[pivot] > a[left], so algorithm moves one position to right as -

  

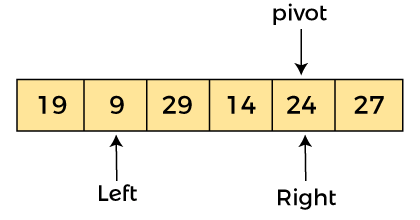
  Now, a[left] = 9, a[right] = 24, and a[pivot] = 24. As a[pivot] > a[left], so algorithm moves one position to right as -

  

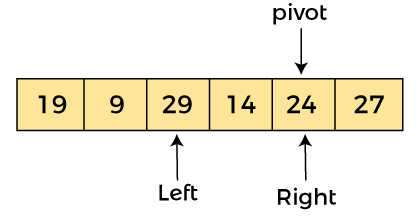
  Now, a[left] = 29, a[right] = 24, and a[pivot] = 24. As a[pivot] < a[left], so, swap a[pivot] and a[left], now pivot is at left, i.e. -

  

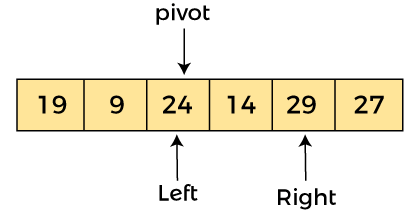
  Since, pivot is at left, so algorithm starts from right, and move to left. Now, a[left] = 24, a[right] = 29, and a[pivot] = 24. As a[pivot] < a[right], so algorithm moves one position to left, as -

  

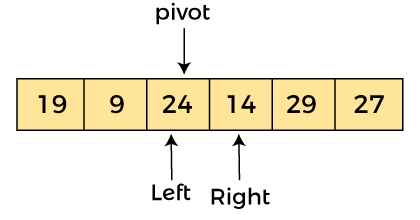
  Now, a[pivot] = 24, a[left] = 24, and a[right] = 14. As a[pivot] > a[right], so, swap a[pivot] and a[right], now pivot is at right, i.e. -

  

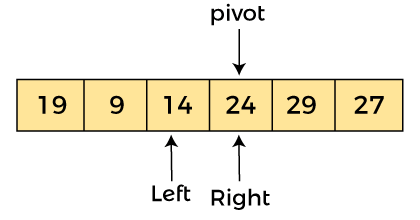
  Now, a[pivot] = 24, a[left] = 14, and a[right] = 24. Pivot is at right, so the algorithm starts from left and move to right.

  

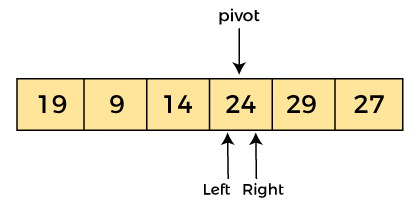
  Now, a[pivot] = 24, a[left] = 24, and a[right] = 24. So, pivot, left and right are pointing the same element. It represents the termination of procedure.

  Element 24, which is the pivot element is placed at its exact position.

  Elements that are right side of element 24 are greater than it, and the elements that are left side of element 24 are smaller than it.

  

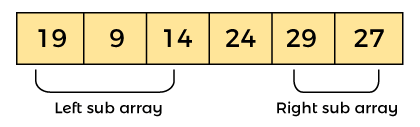
  Now, in a similar manner, quick sort algorithm is separately applied to the left and right sub-arrays. After sorting gets done, the array will be -

  

  Quicksort complexity

  Now, let's see the time complexity of quicksort in best case, average case, and in worst case. We will also see the space complexity of quicksort.

  1. Time Complexity

  | Case | Time Complexity | | --- | --- | | Best Case | O(n*logn) | | Average Case | O(n*logn) | | Worst Case | O(n²) |

Time Complexity:

• Best Case: Ω (N log (N))
  The best-case scenario for quicksort occur when the pivot chosen at the each step divides the array into roughly equal halves.
  In this case, the algorithm will make balanced partitions, leading to efficient Sorting.

• Average Case: θ ( N log (N))
  Quicksort’s average-case performance is usually very good in practice, making it one of the fastest sorting Algorithm.

• Worst Case: O(N2)
  The worst-case Scenario for Quicksort occur when the pivot at each step consistently results in highly unbalanced partitions. When the array is already sorted and the pivot is always chosen as the smallest or largest element. To mitigate the worst-case Scenario, various techniques are used such as choosing a good pivot (e.g., median of three) and using Randomized algorithm (Randomized Quicksort ) to shuffle the element before sorting.

• Auxiliary Space: O(1), if we don’t consider the recursive stack space. If we consider the recursive stack space then, in the worst case quicksort could make O(N).

Advantages of Quick Sort:

• It is a divide-and-conquer algorithm that makes it easier to solve problems.

• It is efficient on large data sets.

• It has a low overhead, as it only requires a small amount of memory to function.

Disadvantages of Quick Sort:

• It has a worst-case time complexity of O(N²), which occurs when the pivot is chosen poorly.

• It is not a good choice for small data sets.

• It is not a stable sort, meaning that if two elements have the same key, their relative order will not be preserved in the sorted output in case of quick sort, because here we are swapping elements according to the pivot’s position (without considering their original positions).