Insertion Sort
InserInsertion sort is a basic sorting method where you place each item from an unsorted list into its proper position in a sorted section of the list. It's a stable sorting method, ensuring that items with the same values stay in their original order in the sorted list.
Imagine sorting playing cards in your hand. You divide the cards into two parts: the sorted ones and the unsorted ones. Then, you take a card from the unsorted group and insert it into the correct spot in the sorted group.
Algorithm
The simple steps of achieving the insertion sort are listed as follows -
Step 1 - If the element is the first element, assume that it is already sorted. Return 1.
Step2 - Pick the next element, and store it separately in a key.
Step3 - Now, compare the key with all elements in the sorted array.
Step 4 - If the element in the sorted array is smaller than the current element, then move to the next element. Else, shift greater elements in the array towards the right.
Step 5 - Insert the value.
Step 6 - Repeat until the array is sorted.
Working of Insertion sort Algorithm
Now, let's delve into the intricacies of the insertion sort algorithm.
To grasp the inner workings of the insertion sort algorithm, let's consider an unsorted array for a more concrete illustration.
Let's assume the array elements are as follows:
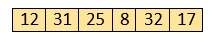
Initially, the first two elements are compared in insertion sort.
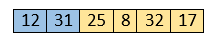
Here, 31 is greater than 12. That means both elements are already in ascending order. So, for now, 12 is stored in a sorted sub-array.
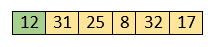
Now, move to the next two elements and compare them.
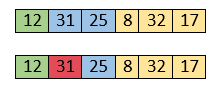
Here, 25 is smaller than 31. So, 31 is not at correct position. Now, swap 31 with 25. Along with swapping, insertion sort will also check it with all elements in the sorted array.
For now, the sorted array has only one element, i.e. 12. So, 25 is greater than 12. Hence, the sorted array remains sorted after swapping.
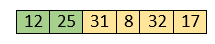
Now, two elements in the sorted array are 12 and 25. Move forward to the next elements that are 31 and 8.
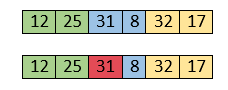
Both 31 and 8 are not sorted. So, swap them.
After swapping, elements 25 and 8 are unsorted.

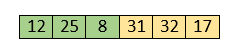
So, swap them.
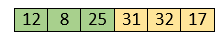
Now, elements 12 and 8 are unsorted.
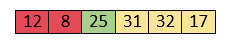
So, swap them too.
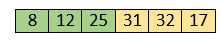
Now, the sorted array has three items that are 8, 12 and 25. Move to the next items that are 31 and 32.

Hence, they are already sorted. Now, the sorted array includes 8, 12, 25 and 31.
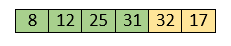
Move to the next elements that are 32 and 17.
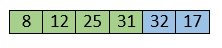
17 is smaller than 32. So, swap them.
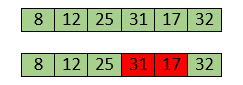
Swapping makes 31 and 17 unsorted. So, swap them too.
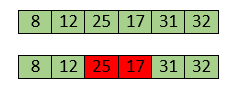
Now, swapping makes 25 and 17 unsorted. So, perform swapping again.
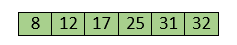
Now, the array is completely sorted.
Insertion Sort Complexity
Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time. It is efficient for small data sets but can be slow for larger lists. In the best-case scenario, when the input array is already sorted, the time complexity of insertion sort is O(n), where n is the number of elements in the array.
In the average case, insertion sort has a time complexity of O(n^2), which means it will take quadratic time to sort the array. This is because, on average, each element will need to be compared and shifted multiple times before reaching its correct position.
In the worst-case scenario, when the input array is sorted in reverse order, the time complexity of insertion sort is also O(n^2). This is because each element will need to be compared and shifted all the way to the beginning of the sorted array.
When it comes to space complexity, insertion sort is an in-place sorting algorithm, meaning it does not require any additional space other than the input array itself. This makes it efficient in terms of space usage, as it sorts the array by moving elements around within the original array without needing extra memory.
1. Time Complexity
| Case | Time Complexity |
| Best Case | O(n) |
| Average Case | O(n2) |
| Worst Case | O(n2) |
Best Case Complexity - It occurs when there is no sorting required, i.e. the array is already sorted. The best-case time complexity of insertion sort is O(n).
Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of insertion sort is O(n2).
Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of insertion sort is O(n2).
2. Space Complexity
| Space Complexity | O(1) |
| Stable | YES |
- The space complexity of insertion sort is O(1). It is because, in insertion sort, an extra variable is required for swapping.
Advantages of Insertion Sort:
Simple and easy to implement.
Stable sorting algorithm.
Efficient for small lists and nearly sorted lists.
Space-efficient.
Disadvantages of Insertion Sort:
Inefficient for large lists.
Not as efficient as other sorting algorithms (e.g., merge sort, quick sort) for most cases.
Applications of Insertion Sort:
Insertion sort is commonly used in situations where:
The list is small or nearly sorted.
Simplicity and stability are important.