Heap Sort
Heap sort processes the elements by creating the min-heap or max-heap using the elements of the given array. Min-heap or max-heap represents the ordering of array in which the root element represents the minimum or maximum element of the array.
Heap sort basically recursively performs two main operations -
Build a heap H, using the elements of array.
Repeatedly delete the root element of the heap formed in 1st phase.
Before knowing more about the heap sort, let's first see a brief description of Heap.
What is a heap?
A heap is a complete binary tree, and the binary tree is a tree in which the node can have the utmost two children. A complete binary tree is a binary tree in which all the levels except the last level, i.e., leaf node, should be completely filled, and all the nodes should be left-justified.
What is heap sort?
Heapsort is a popular and efficient sorting algorithm. The concept of heap sort is to eliminate the elements one by one from the heap part of the list, and then insert them into the sorted part of the list.
Heapsort is the in-place sorting algorithm.
Heap Sort Algorithm
To solve the problem follow the below idea:
First, turn the array into a heap using heapify. Then, delete the root node of the Max-heap one by one, replace it with the last node in the heap, and heapify the root. Repeat this until the heap has only one element left.
Build a heap from the input array.
Repeat these steps until the heap has only one element:
Swap the root element (the largest) with the last element of the heap.
Remove the last element (now in the correct position).
Heapify the remaining elements.
The sorted array is obtained by reversing the order of the elements in the input array.
In heap sort, basically, there are two phases involved in the sorting of elements. By using the heap sort algorithm, they are as follows -
The first step includes the creation of a heap by adjusting the elements of the array.
After the creation of heap, now remove the root element of the heap repeatedly by shifting it to the end of the array, and then store the heap structure with the remaining elements.
Now let's see the working of heap sort in detail by using an example. To understand it more clearly, let's take an unsorted array and try to sort it using heap sort. It will make the explanation clearer and easier.

First, we have to construct a heap from the given array and convert it into max heap.
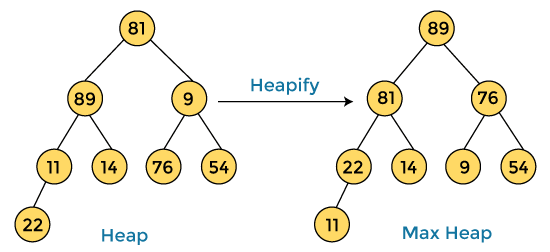
After converting the given heap into max heap, the array elements are -

Next, we have to delete the root element (89) from the max heap. To delete this node, we have to swap it with the last node, i.e. (11). After deleting the root element, we again have to heapify it to convert it into max heap.
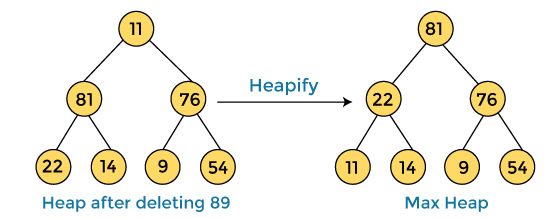
After swapping the array element 89 with 11, and converting the heap into max-heap, the elements of array are -

In the next step, again, we have to delete the root element (81) from the max heap. To delete this node, we have to swap it with the last node, i.e. (54). After deleting the root element, we again have to heapify it to convert it into max heap.
ADVERTISEMENT
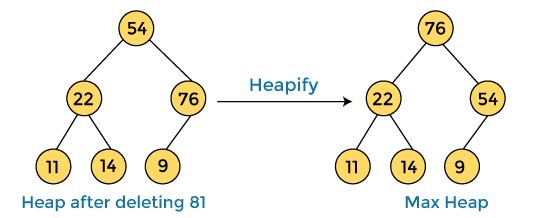
After swapping the array element 81 with 54 and converting the heap into max-heap, the elements of array are -

In the next step, we have to delete the root element (76) from the max heap again. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap.
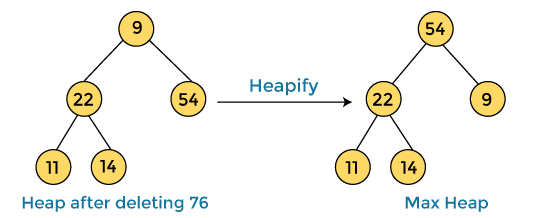
After swapping the array element 76 with 9 and converting the heap into max-heap, the elements of array are -

In the next step, again we have to delete the root element (54) from the max heap. To delete this node, we have to swap it with the last node, i.e. (14). After deleting the root element, we again have to heapify it to convert it into max heap.
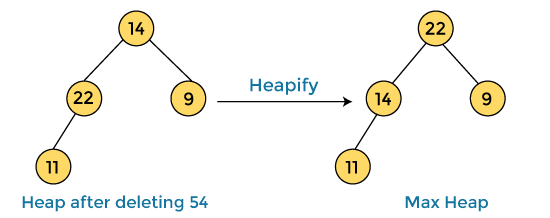
After swapping the array element 54 with 14 and converting the heap into max-heap, the elements of array are -

ADVERTISEMENT
In the next step, again we have to delete the root element (22) from the max heap. To delete this node, we have to swap it with the last node, i.e. (11). After deleting the root element, we again have to heapify it to convert it into max heap.
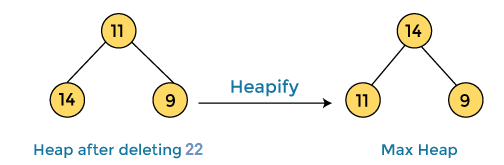
After swapping the array element 22 with 11 and converting the heap into max-heap, the elements of array are -

In the next step, again we have to delete the root element (14) from the max heap. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap.
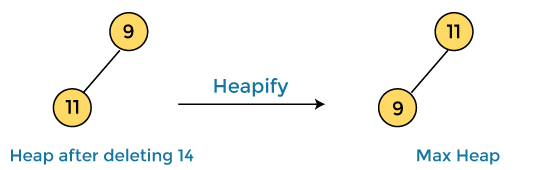
After swapping the array element 14 with 9 and converting the heap into max-heap, the elements of array are -

In the next step, again we have to delete the root element (11) from the max heap. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap.

After swapping the array element 11 with 9, the elements of array are -

Now, heap has only one element left. After deleting it, heap will be empty.

After completion of sorting, the array elements are -

Now, the array is completely sorted.
Complexity Analysis of Heap Sort
Time Complexity: O(N log N)
Auxiliary Space: O(log n), due to the recursive call stack. However, auxiliary space can be O(1) for iterative implementation.
Important points about Heap Sort:
Heap sort is an in-place algorithm.
Its typical implementation is not stable but can be made stable (See this)
Typically 2-3 times slower than well-implemented QuickSort. The reason for slowness is a lack of locality of reference.
Advantages of Heap Sort:
Efficient Time Complexity: Heap Sort has a time complexity of O(n log n) in all cases. This makes it good for sorting large datasets. The log n factor comes from the height of the binary heap, ensuring the algorithm stays fast even with many elements.
Memory Usage: Memory usage can be minimal if you use an iterative heapify() instead of a recursive one. So, besides the memory needed to hold the initial list of items to be sorted, it doesn't need extra memory space to work.
Simplicity: It is easier to understand than other equally efficient sorting algorithms because it doesn't use advanced concepts like recursion.
Disadvantages of Heap Sort:
Costly: Heap sort is expensive because it has higher constants compared to merge sort, even though both have a time complexity of O(n log n).
Unstable: Heap sort is unstable and might change the order of equal elements.
Not Efficient for Complex Data: Heap sort is not very efficient when dealing with highly complex data.