Bubble Sort
Bubble sort is a basic sorting method. It works by comparing pairs of neighboring elements and swapping them if they are not in the correct order. This method is not efficient for sorting large amounts of data because its average and worst-case complexity are O(n2), where n represents the number of items.
Here's how the Bubble Sort algorithm works:
Start from the beginning and compare neighboring elements, moving the larger one to the right.
Repeat this process to move the largest element to the far right.
Continue this process to sort the data by finding the next largest element and placing it correctly, and so on.
Working of Bubble sort Algorithm
Let the elements of array are -
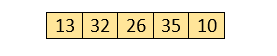
1. First Pass
Sorting begins with the first two elements. We compare them to see which one is larger.
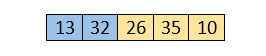
Here, 32 is greater than 13 (32 > 13), so it is already sorted. Now, compare 32 with 26.
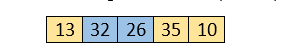
Here, 26 is smaller than 36. So, swapping is required. After swapping new array will look like -
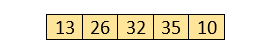
Now, compare 32 and 35.

Here, 35 is greater than 32. So, there is no swapping required as they are already sorted.
Now, the comparison will be in between 35 and 10.
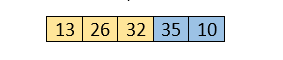
Here, 10 is smaller than 35 that are not sorted. So, swapping is required. Now, we reach at the end of the array. After first pass, the array will be -
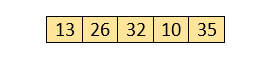
Now, move to the second iteration.
2.Second Pass
The same process will be followed for second iteration.
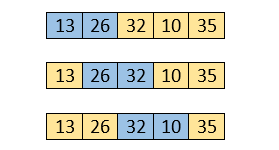
Here, 10 is smaller than 32. So, swapping is required. After swapping, the array will be -
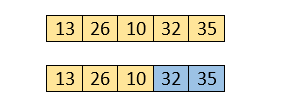
Now, move to the third iteration.
3.Third Pass
The same process will be followed for third iteration.
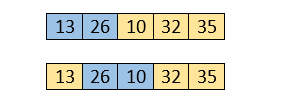
Here, 10 is smaller than 26. So, swapping is required. After swapping, the array will be -
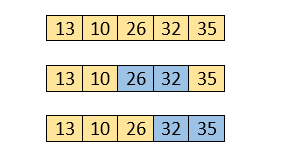
Now, move to the fourth iteration.
4.Fourth pass
Similarly, after the fourth iteration, the array will be -
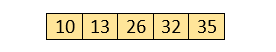
Hence, there is no swapping required, so the array is completely sorted.
Bubble Sort Implementation
To implement the Bubble Sort algorithm in a programming language, we need:
An array with values to sort.
An inner loop that goes through the array and swaps values if the first value is higher than the next value. This loop must loop through one less value each time it runs.
An outer loop that controls how many times the inner loop must run. For an array with n values, this outer loop must run n-1 times.
Bubble sort complexity
Time complexity of bubble sort varies in different scenarios: best case, average case, and worst case. We will also discuss the space complexity of bubble sort.
1. Time Complexity
| Case | Time Complexity |
| Best Case | O(n) |
| Average Case | O(n2) |
| Worst Case | O(n2) |
Best Case Complexity - This happens when no sorting is needed, meaning the array is already sorted. The best-case time complexity of bubble sort is O(n).
Average Case Complexity - This occurs when the array elements are in a mixed-up order, not properly in ascending or descending order. The average case time complexity of bubble sort is O(n2).
Worst Case Complexity - This occurs when the array elements need to be sorted in reverse order. For example, if you need to sort the array elements in ascending order, but they are in descending order. The worst-case time complexity of bubble sort is O(n2).
2. Space Complexity
| Space Complexity | O(1) |
| Stable | YES |
The space complexity of bubble sort is O(1). It is because, in bubble sort, an extra variable is required for swapping.
The space complexity of optimized bubble sort is O(2). It is because two extra variables are required in optimized bubble sort.
Advantages of Bubble Sort:
Bubble sort is easy to understand and use.
It doesn't need extra memory space.
It's a stable sorting method, meaning elements with the same key value keep their order in the sorted result.
Disadvantages of Bubble Sort:
Bubble sort is slow for big data sets due to its O(N2) time complexity.
It relies on comparisons to sort elements, which can affect its efficiency in some situations.